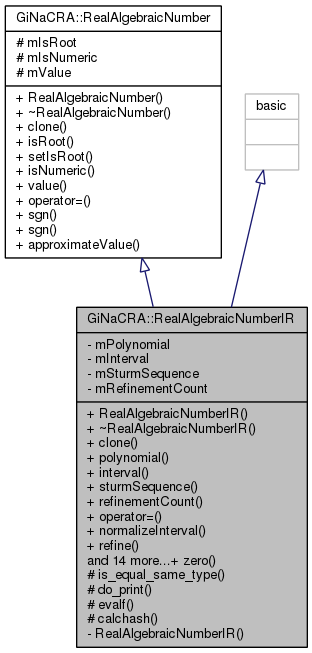
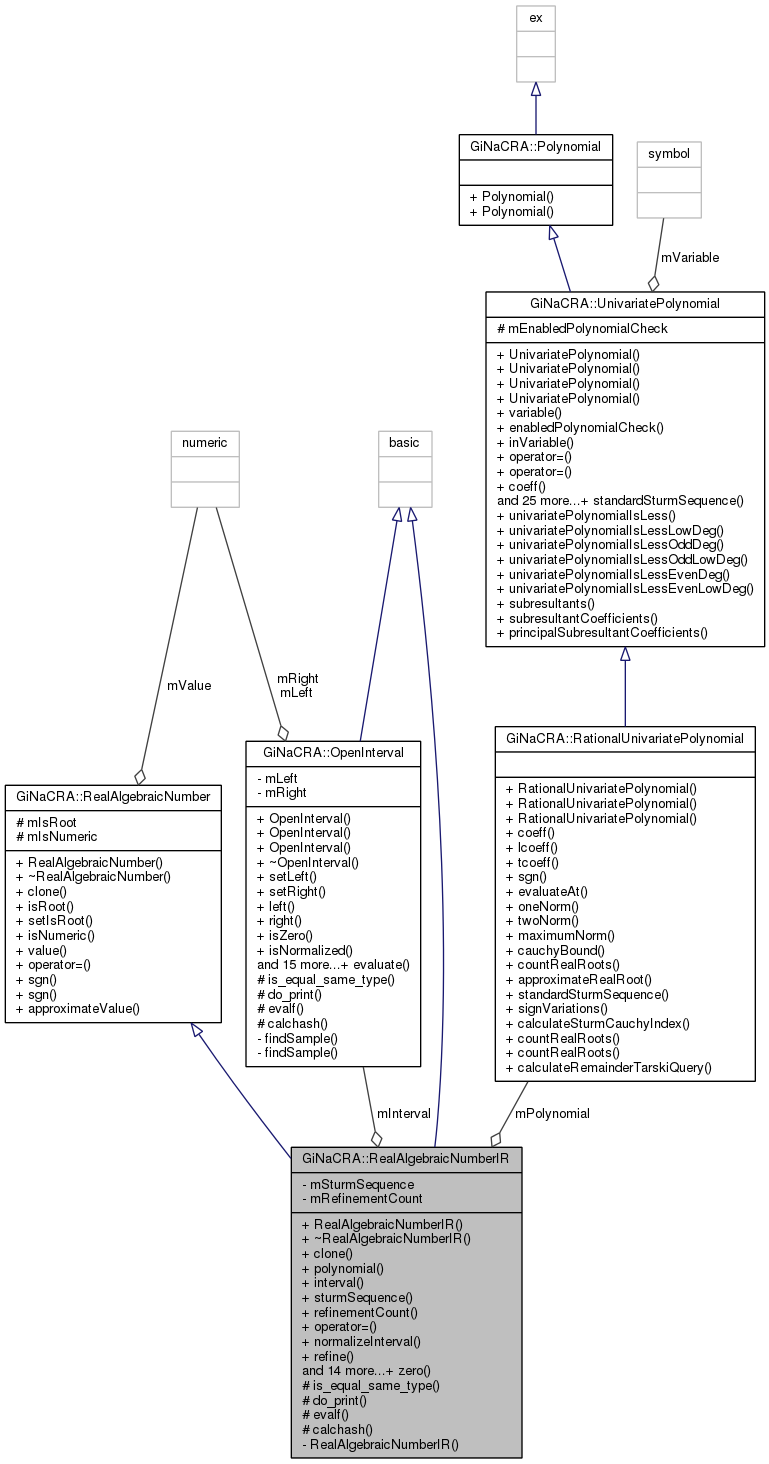
An implementation of an real algebraic number providing methods to add, multiply or evaluate their sign on polynomials. More...

#include <RealAlgebraicNumberIR.h>

Inheritance diagram for GiNaCRA::RealAlgebraicNumberIR:

[legend]

Collaboration diagram for GiNaCRA::RealAlgebraicNumberIR:

[legend]

Public Member Functions
	RealAlgebraicNumberIR (const RationalUnivariatePolynomial &p, const OpenInterval &i, const list< RationalUnivariatePolynomial > &s=list< RationalUnivariatePolynomial >(), const bool normalize=true, const bool isRoot=true) throw ( invalid_argument )
	Constructs a real algebraic number in interval representation (p, l, r) with a normalized interval w.r.t.
	~RealAlgebraicNumberIR ()
	Destructor.
RealAlgebraicNumberPtr	clone () const
	Clone-"Constructor".
const RationalUnivariatePolynomial	polynomial () const
	Selects the polynomial having this real algebraic number as one of its roots.
const OpenInterval	interval () const
	Selects the open interval ]l, r[ containing the real algebraic number.
const list < RationalUnivariatePolynomial >	sturmSequence () const
	Returns a pre-computed standard Sturm sequence of the polynomial and its derivative.
const unsigned	refinementCount () const
	Returns how often one of the refine methods was called before.
const RealAlgebraicNumberIR &	operator= (const RealAlgebraicNumberIR &)
	This number gets all values of the other.
void	normalizeInterval () throw ( invalid_argument )
	Normalizes the interval of an real algebraic number to not contain zero, in case the number is non-zero.
void	refine (RealAlgebraicNumberSettings::RefinementStrategy strategy=RealAlgebraicNumberSettings::DEFAULT_REFINEMENTSTRATEGY)
	Refines the interval i of this real algebraic number yielding the interval j such that `2*(j.Right()-j.Left()) <= i.Right()-i.Left()`.
void	refine (numeric eps)
	Refines the interval i of this real algebraic number yielding the interval j such that `(j.Right()-j.Left()) <= eps`.
bool	refineAvoiding (numeric n)
	Refines the interval i of this real algebraic number yielding the interval j such that !j.meets(n).
GiNaC::sign	sgn () const
	Returns sign (GiNaC::ZERO_SIGN, GiNaC::POSITIVE_SIGN, GiNaC::NEGATIVE_SIGN) of this real algebraic number.
GiNaC::sign	sgn (const RationalUnivariatePolynomial &p) const
	Returns sign (GiNaC::ZERO_SIGN, GiNaC::POSITIVE_SIGN, GiNaC::NEGATIVE_SIGN) of the specified univariate polynomial at this real algebraic number.
const numeric	approximateValue () const
	Computes a numeric value for this real algebraic number approximating it.
const numeric	sampleValue () const
	Chooses a numeric value out of the isolating interval with the smallest numeric representation.
RealAlgebraicNumberIR &	add (RealAlgebraicNumberIR &o) throw ( invalid_argument )
	Adds two real algebraic numbers and returns a reference to their sum.
RealAlgebraicNumberIR &	minus () const
	Returns the negative value.
RealAlgebraicNumberIR &	mul (RealAlgebraicNumberIR &o) throw ( invalid_argument )
	Multiplies two real algebraic numbers and returns a reference to their product.
RealAlgebraicNumberIR &	inverse () const throw ( invalid_argument )
	Returns the inverse.
RealAlgebraicNumberIR &	pow (int e) throw ( invalid_argument )
	Returns the power.
const bool	isEqual (RealAlgebraicNumberIR &o)
	Compares two real algebraic numbers for equality.
const bool	isLessWhileUnequal (RealAlgebraicNumberIR &o)
	Checks whether this number is less than the other while assuming that the two numbers are unequal.
const bool	isLess (RealAlgebraicNumberIR &o)
	Compares two real algebraic numbers by less-than.
bool	info (unsigned inf) const
const bool	isRoot () const
void	setIsRoot (bool isRoot)
	Set the flag marking whether the real algebraic number stems from a root computation or not.
bool	isNumeric () const
	Returns true if an exact numeric representation was found during the refinements.
const numeric	value () const
	Gives an exact numeric representation of this real algebraic number which could have been found during the refinement steps.
Static Public Member Functions
static RealAlgebraicNumberIR *	zero (const symbol &s)
Protected Member Functions
bool	is_equal_same_type (const basic &other) const
void	do_print (const print_context &c, unsigned level=0) const
ex	evalf (int level=0) const
	Outputs the midpoint of the isolating interval after `level` additional refinements.
unsigned	calchash () const
Protected Attributes
bool	mIsRoot
	flag indicating whether this number represents a root of a polynomial or an intermediate point
bool	mIsNumeric
	flag indicating whether this number is representable by a numeric
numeric	mValue
	the exact numeric value of this number if available, otherwise mIsNumeric is false and mValue 0
Private Member Functions
	RealAlgebraicNumberIR (const symbol &s) throw ( invalid_argument )
	Private zero constructor.
Private Attributes
RationalUnivariatePolynomial	mPolynomial
	polynomial of this interval representation
OpenInterval	mInterval
	isolating interval of this interval representation
list < RationalUnivariatePolynomial >	mSturmSequence
	Standard Sturm sequence of the polynomial and its derivative.
unsigned	mRefinementCount
	number of refinements executed to the isolating interval

Detailed Description

An implementation of an real algebraic number providing methods to add, multiply or evaluate their sign on polynomials.

Author:: Ulrich Loup

Since:: 2010-07-28

Version:: 2012-05-07

See also:: ISBN 0-387-94090-1 and ISBN-13: 978-3642069642

Definition at line 52 of file RealAlgebraicNumberIR.h.

Constructor & Destructor Documentation

GiNaCRA::RealAlgebraicNumberIR::RealAlgebraicNumberIR	(	const RationalUnivariatePolynomial &	p,
		const OpenInterval &	i,
		const list< RationalUnivariatePolynomial > &	s = `list<RationalUnivariatePolynomial>()`,
		const bool	normalize = `true`,
		const bool	isRoot = `true`
	)		throw ( invalid_argument )

Constructs a real algebraic number in interval representation (p, l, r) with a normalized interval w.r.t.

normalizeInterval. Constructs a real algebraic number in interval and order representation (p, l, r, o) with a normalized interval w.r.t. normalizeInterval.

p can be changed within the constructor, but is later constant.
i can be changed later by refine(), but is only normalized within the constructor in case not normalized before.

Parameters:

p	polynomial having the real algebraic number as one of its roots
i	open interval ]l, r[ containing the real algebraic number (should be normalized)
s	standard Sturm sequence
normalize	if set to false, the interval will not be normalized in the constructor (default is true)
isRoot	true marks this real algebraic number to stem from a root computation

Definition at line 75 of file RealAlgebraicNumberIR.cpp.

Referenced by clone(), inverse(), minus(), and zero().

GiNaCRA::RealAlgebraicNumberIR::~RealAlgebraicNumberIR ( )

Destructor.

Definition at line 111 of file RealAlgebraicNumberIR.cpp.

GiNaCRA::RealAlgebraicNumberIR::RealAlgebraicNumberIR ( const symbol & s ) throw ( invalid_argument ) [private]

Private zero constructor.

Parameters:

s	main symbol of the polynomial belonging to the real algebraic number

Definition at line 65 of file RealAlgebraicNumberIR.cpp.

Member Function Documentation

RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::add ( RealAlgebraicNumberIR & o ) throw ( invalid_argument )

Adds two real algebraic numbers and returns a reference to their sum.

Parameters:

o

Returns:: sum

Definition at line 403 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::UnivariatePolynomial::diff(), interval(), GiNaCRA::OpenInterval::isZero(), mInterval, mPolynomial, GiNaCRA::UnivariatePolynomial::primpart(), refine(), GiNaCRA::RationalUnivariatePolynomial::signVariations(), GiNaCRA::RationalUnivariatePolynomial::standardSturmSequence(), and GiNaCRA::UnivariatePolynomial::variable().

Referenced by isEqual(), GiNaCRA::operator+(), and GiNaCRA::operator-().

const numeric GiNaCRA::RealAlgebraicNumberIR::approximateValue ( ) const [inline, virtual]

Computes a numeric value for this real algebraic number approximating it.

This is also the outcome of ex::evalf().

Runtime complexity:: constant

Returns:: a numeric value for this real algebraic number approximating it

Reimplemented from GiNaCRA::RealAlgebraicNumber.

Definition at line 202 of file RealAlgebraicNumberIR.h.

References GiNaCRA::OpenInterval::midpoint(), and mInterval.

Referenced by evalf().

unsigned GiNaCRA::RealAlgebraicNumberIR::calchash ( ) const [protected]

Definition at line 169 of file RealAlgebraicNumberIR.cpp.

References mPolynomial.

RealAlgebraicNumberPtr GiNaCRA::RealAlgebraicNumberIR::clone ( ) const [virtual]

Clone-"Constructor".

Reimplemented from GiNaCRA::RealAlgebraicNumber.

Definition at line 113 of file RealAlgebraicNumberIR.cpp.

References RealAlgebraicNumberIR().

void GiNaCRA::RealAlgebraicNumberIR::do_print	(	const print_context &	c,
		unsigned	level = `0`
	)		const `[protected]`

Definition at line 149 of file RealAlgebraicNumberIR.cpp.

References mInterval, GiNaCRA::RealAlgebraicNumber::mIsNumeric, GiNaCRA::RealAlgebraicNumber::mIsRoot, mPolynomial, and GiNaCRA::RealAlgebraicNumber::mValue.

ex GiNaCRA::RealAlgebraicNumberIR::evalf ( int level = 0 ) const [protected]

Outputs the midpoint of the isolating interval after level additional refinements.

Note that the refinements are not performed on this object but on a copy since this method does not mute this object.

Parameters:

level number of additional refinements

Returns:: midpoint of the isolating interval after level additional refinements

Definition at line 157 of file RealAlgebraicNumberIR.cpp.

References approximateValue(), GiNaCRA::OpenInterval::midpoint(), mInterval, and refine().

bool GiNaCRA::RealAlgebraicNumberIR::info ( unsigned inf ) const

Definition at line 174 of file RealAlgebraicNumberIR.cpp.

const OpenInterval GiNaCRA::RealAlgebraicNumberIR::interval ( ) const [inline]

Selects the open interval ]l, r[ containing the real algebraic number.

Returns:: open interval ]l, r[ containing the real algebraic number

Definition at line 120 of file RealAlgebraicNumberIR.h.

References mInterval.

Referenced by add(), is_equal_same_type(), isEqual(), mul(), GiNaCRA::operator*(), GiNaCRA::operator+(), and GiNaCRA::operator-().

RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::inverse ( ) const throw ( invalid_argument )

Returns the inverse.

Returns:: inverse value

Definition at line 456 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::UnivariatePolynomial::degree(), GiNaCRA::OpenInterval::left(), mInterval, mPolynomial, RealAlgebraicNumberIR(), GiNaCRA::OpenInterval::right(), and GiNaCRA::UnivariatePolynomial::variable().

Referenced by normalizeInterval(), and GiNaCRA::operator/().

bool GiNaCRA::RealAlgebraicNumberIR::is_equal_same_type ( const basic & other ) const [protected]

Definition at line 133 of file RealAlgebraicNumberIR.cpp.

References interval(), GiNaCRA::OpenInterval::isZero(), GiNaCRA::OpenInterval::left(), mInterval, GiNaCRA::RealAlgebraicNumber::mIsNumeric, GiNaCRA::RealAlgebraicNumber::mValue, and GiNaCRA::OpenInterval::right().

const bool GiNaCRA::RealAlgebraicNumberIR::isEqual ( RealAlgebraicNumberIR & o )

Compares two real algebraic numbers for equality.

Note that both numbers could be muted by means of refinement!

Parameters:

o

Returns:: true in case the other real algebraic number is equals to this one

Definition at line 496 of file RealAlgebraicNumberIR.cpp.

References add(), interval(), GiNaCRA::OpenInterval::isZero(), GiNaCRA::OpenInterval::left(), mInterval, minus(), GiNaCRA::RealAlgebraicNumber::mIsNumeric, GiNaCRA::RealAlgebraicNumber::mValue, and GiNaCRA::OpenInterval::right().

Referenced by isLess(), GiNaCRA::operator!=(), GiNaCRA::operator<=(), GiNaCRA::operator==(), and GiNaCRA::operator>().

const bool GiNaCRA::RealAlgebraicNumberIR::isLess ( RealAlgebraicNumberIR & o )

Compares two real algebraic numbers by less-than.

Note that both numbers could be muted by means of refinement!

Parameters:

o	reference to the other real algebraic number.

Returns:: true in case the other real algebraic number is strictly less than this one

Definition at line 532 of file RealAlgebraicNumberIR.cpp.

References isEqual(), and isLessWhileUnequal().

Referenced by GiNaCRA::operator<(), and GiNaCRA::operator>=().

const bool GiNaCRA::RealAlgebraicNumberIR::isLessWhileUnequal ( RealAlgebraicNumberIR & o )

Checks whether this number is less than the other while assuming that the two numbers are unequal.

Note that both numbers could be muted by means of refinement!

Parameters:

o

Returns:: true in case the other real algebraic number is less to this one if the two number do not equal (otherwise there might be an infinite refinement loop)

Check whether -----]--------[---------------- --------------]--------[------- .

Check whether --------------]--------[------- -----]--------[---------------- .

Todo:
improve search

Definition at line 507 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::left(), mInterval, refine(), and GiNaCRA::OpenInterval::right().

Referenced by isLess(), GiNaCRA::operator<=(), and GiNaCRA::operator>().

bool GiNaCRA::RealAlgebraicNumber::isNumeric ( ) const [inline, inherited]

Returns true if an exact numeric representation was found during the refinements.

Returns:: true if an exact numeric representation was found during the refinements, false otherwise.

Definition at line 96 of file RealAlgebraicNumber.h.

References GiNaCRA::RealAlgebraicNumber::mIsNumeric.

Referenced by GiNaCRA::binaryOperator().

const bool GiNaCRA::RealAlgebraicNumber::isRoot ( ) const [inline, inherited]

Returns:: the flag marking whether the real algebraic number stems from a root computation or not

Definition at line 78 of file RealAlgebraicNumber.h.

References GiNaCRA::RealAlgebraicNumber::mIsRoot.

Referenced by GiNaCRA::RealAlgebraicNumber::setIsRoot().

RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::minus ( ) const

Returns the negative value.

Returns:: negative value

Definition at line 424 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::isZero(), mInterval, mPolynomial, RealAlgebraicNumberIR(), and GiNaCRA::UnivariatePolynomial::variable().

Referenced by isEqual(), and GiNaCRA::operator-().

RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::mul ( RealAlgebraicNumberIR & o ) throw ( invalid_argument )

Multiplies two real algebraic numbers and returns a reference to their product.

Parameters:

o

Returns:: product

Definition at line 433 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::UnivariatePolynomial::diff(), interval(), GiNaCRA::OpenInterval::isZero(), mInterval, mPolynomial, GiNaCRA::UnivariatePolynomial::primpart(), refine(), GiNaCRA::RationalUnivariatePolynomial::signVariations(), GiNaCRA::RationalUnivariatePolynomial::standardSturmSequence(), and GiNaCRA::UnivariatePolynomial::variable().

Referenced by GiNaCRA::operator*(), GiNaCRA::operator/(), and pow().

void GiNaCRA::RealAlgebraicNumberIR::normalizeInterval ( ) throw ( invalid_argument )

Normalizes the interval of an real algebraic number to not contain zero, in case the number is non-zero.

Definition at line 214 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::contains(), inverse(), GiNaCRA::OpenInterval::isZero(), GiNaCRA::OpenInterval::left(), GiNaCRA::RationalUnivariatePolynomial::maximumNorm(), mInterval, mPolynomial, mSturmSequence, GiNaCRA::OpenInterval::right(), GiNaCRA::OpenInterval::setLeft(), GiNaCRA::OpenInterval::setRight(), and GiNaCRA::RationalUnivariatePolynomial::signVariations().

const RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::operator= ( const RealAlgebraicNumberIR & o )

This number gets all values of the other.

Definition at line 195 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::contains(), mInterval, GiNaCRA::RealAlgebraicNumber::mIsNumeric, GiNaCRA::RealAlgebraicNumber::mIsRoot, mPolynomial, mRefinementCount, mSturmSequence, and GiNaCRA::RealAlgebraicNumber::mValue.

const RationalUnivariatePolynomial GiNaCRA::RealAlgebraicNumberIR::polynomial ( ) const [inline]

Selects the polynomial having this real algebraic number as one of its roots.

Returns:: polynomial having the number as one of its roots

Definition at line 111 of file RealAlgebraicNumberIR.h.

References mPolynomial.

Referenced by GiNaCRA::operator*(), GiNaCRA::operator+(), and GiNaCRA::operator-().

RealAlgebraicNumberIR & GiNaCRA::RealAlgebraicNumberIR::pow ( int e ) throw ( invalid_argument )

Returns the power.

Parameters:

e

Returns:: inverse value

Definition at line 465 of file RealAlgebraicNumberIR.cpp.

References mul().

Referenced by GiNaCRA::operator^().

void GiNaCRA::RealAlgebraicNumberIR::refine ( RealAlgebraicNumberSettings::RefinementStrategy strategy = RealAlgebraicNumberSettings::DEFAULT_REFINEMENTSTRATEGY )

Refines the interval i of this real algebraic number yielding the interval j such that 2*(j.Right()-j.Left()) <= i.Right()-i.Left().

This is cutting the interval in the middle and choosing the half where the root lays in.

Parameters:

strategy strategy selection according to RealAlgebraicNumberFactory::searchRealRootsStrategy

Runtime complexity:: constant

Space complexity:: constant

Definition at line 233 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::RationalUnivariatePolynomial::approximateRealRoot(), GiNaCRA::RealAlgebraicNumberSettings::BINARYNEWTON_REFINEMENTSTRATEGY, GiNaCRA::RealAlgebraicNumberSettings::BINARYSAMPLE_REFINEMENTSTRATEGY, GiNaCRA::RealAlgebraicNumberSettings::BINNARYMIDPOINTSAMPLE_REFINEMENTSTRATEGY, GiNaCRA::RealAlgebraicNumberSettings::GENERIC_REFINEMENTSTRATEGY, GiNaCRA::OpenInterval::left(), GiNaCRA::RealAlgebraicNumberSettings::MAXREFINE_REFINEMENTSTRATEGY, GiNaCRA::OpenInterval::midpoint(), mInterval, GiNaCRA::RealAlgebraicNumber::mIsNumeric, mPolynomial, mRefinementCount, mSturmSequence, GiNaCRA::RealAlgebraicNumber::mValue, GiNaCRA::OpenInterval::right(), GiNaCRA::OpenInterval::sample(), GiNaCRA::OpenInterval::setLeft(), GiNaCRA::OpenInterval::setRight(), GiNaCRA::RationalUnivariatePolynomial::sgn(), GiNaCRA::RationalUnivariatePolynomial::signVariations(), and GiNaC::ZERO_SIGN.

Referenced by add(), evalf(), isLessWhileUnequal(), mul(), GiNaCRA::operator*(), GiNaCRA::operator+(), GiNaCRA::operator-(), and refine().

void GiNaCRA::RealAlgebraicNumberIR::refine ( numeric eps ) [inline]

Refines the interval i of this real algebraic number yielding the interval j such that (j.Right()-j.Left()) <= eps.

Parameters:

eps

Definition at line 171 of file RealAlgebraicNumberIR.h.

References GiNaCRA::OpenInterval::left(), mInterval, refine(), and GiNaCRA::OpenInterval::right().

bool GiNaCRA::RealAlgebraicNumberIR::refineAvoiding ( numeric n )

Refines the interval i of this real algebraic number yielding the interval j such that !j.meets(n).

If true is returned, n is the exact numeric representation of this root. Otherwise not.

Parameters:

n

Runtime complexity:: constant

Space complexity:: constant

Returns:: true, if n is the exact numeric representation of this root, otherwise false

Definition at line 280 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::contains(), GiNaCRA::RationalUnivariatePolynomial::countRealRoots(), GiNaCRA::OpenInterval::left(), GiNaCRA::OpenInterval::meets(), mInterval, GiNaCRA::RealAlgebraicNumber::mIsNumeric, mPolynomial, mRefinementCount, mSturmSequence, GiNaCRA::RealAlgebraicNumber::mValue, GiNaCRA::OpenInterval::right(), GiNaCRA::OpenInterval::sampleFast(), GiNaCRA::OpenInterval::setLeft(), GiNaCRA::OpenInterval::setRight(), GiNaCRA::RationalUnivariatePolynomial::sgn(), GiNaCRA::RationalUnivariatePolynomial::signVariations(), and GiNaC::ZERO_SIGN.

const unsigned GiNaCRA::RealAlgebraicNumberIR::refinementCount ( ) const [inline]

Returns how often one of the refine methods was called before.

Returns:: number of refinement steps executed on this real algebraic number

Definition at line 137 of file RealAlgebraicNumberIR.h.

References mRefinementCount.

const numeric GiNaCRA::RealAlgebraicNumberIR::sampleValue ( ) const [inline]

Chooses a numeric value out of the isolating interval with the smallest numeric representation.

Runtime complexity:: constant

Returns:: a numeric value for this real algebraic representing a good sample

Definition at line 211 of file RealAlgebraicNumberIR.h.

References mInterval, and GiNaCRA::OpenInterval::sample().

void GiNaCRA::RealAlgebraicNumber::setIsRoot ( bool isRoot ) [inline, inherited]

Set the flag marking whether the real algebraic number stems from a root computation or not.

Parameters:

isRoot

Definition at line 87 of file RealAlgebraicNumber.h.

References GiNaCRA::RealAlgebraicNumber::isRoot(), and GiNaCRA::RealAlgebraicNumber::mIsRoot.

GiNaC::sign GiNaCRA::RealAlgebraicNumberIR::sgn ( ) const [virtual]

Returns sign (GiNaC::ZERO_SIGN, GiNaC::POSITIVE_SIGN, GiNaC::NEGATIVE_SIGN) of this real algebraic number.

Returns:: sign of this real algebraic number.

Reimplemented from GiNaCRA::RealAlgebraicNumber.

Definition at line 367 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::OpenInterval::isZero(), GiNaCRA::OpenInterval::left(), mInterval, GiNaC::NEGATIVE_SIGN, GiNaC::POSITIVE_SIGN, and GiNaC::ZERO_SIGN.

GiNaC::sign GiNaCRA::RealAlgebraicNumberIR::sgn ( const RationalUnivariatePolynomial & p ) const [virtual]

Returns sign (GiNaC::ZERO_SIGN, GiNaC::POSITIVE_SIGN, GiNaC::NEGATIVE_SIGN) of the specified univariate polynomial at this real algebraic number.

Parameters:

p	rational univariate polynomial

Returns:: sign of the univariate polynomial at this real algebraic number.

Reimplemented from GiNaCRA::RealAlgebraicNumber.

Definition at line 376 of file RealAlgebraicNumberIR.cpp.

References GiNaCRA::UnivariatePolynomial::diff(), GiNaCRA::UnivariatePolynomial::isCompatible(), mInterval, mPolynomial, GiNaC::NEGATIVE_SIGN, GiNaC::POSITIVE_SIGN, GiNaCRA::RationalUnivariatePolynomial::signVariations(), GiNaCRA::RationalUnivariatePolynomial::standardSturmSequence(), GiNaCRA::UnivariatePolynomial::variable(), and GiNaC::ZERO_SIGN.

const list<RationalUnivariatePolynomial> GiNaCRA::RealAlgebraicNumberIR::sturmSequence ( ) const [inline]

Returns a pre-computed standard Sturm sequence of the polynomial and its derivative.

Returns:: standard Sturm sequence of the polynomial and its derivative.

Definition at line 129 of file RealAlgebraicNumberIR.h.

References mSturmSequence.

const numeric GiNaCRA::RealAlgebraicNumber::value ( ) const [inline, inherited]

Gives an exact numeric representation of this real algebraic number which could have been found during the refinement steps.

The method returns 0 if the value was never set during refinement.

Returns:: an exact numeric representation of this real algebraic number which could have been found during the refinement steps

Definition at line 105 of file RealAlgebraicNumber.h.

References GiNaCRA::RealAlgebraicNumber::mValue.

Referenced by GiNaCRA::binaryOperator(), and GiNaCRA::RealAlgebraicNumberFactory::less().

RealAlgebraicNumberIR * GiNaCRA::RealAlgebraicNumberIR::zero ( const symbol & s ) [static]

Parameters:

s	the main variable of the underlying polynomial

Returns:: the RealAlgebraicNumberIR representation for 0

Definition at line 543 of file RealAlgebraicNumberIR.cpp.

References RealAlgebraicNumberIR().

Referenced by GiNaCRA::operator*().

Field Documentation

OpenInterval GiNaCRA::RealAlgebraicNumberIR::mInterval [private]

isolating interval of this interval representation

Definition at line 317 of file RealAlgebraicNumberIR.h.

Referenced by add(), approximateValue(), do_print(), evalf(), interval(), inverse(), is_equal_same_type(), isEqual(), isLessWhileUnequal(), minus(), mul(), normalizeInterval(), operator=(), refine(), refineAvoiding(), sampleValue(), and sgn().

bool GiNaCRA::RealAlgebraicNumber::mIsNumeric [protected, inherited]

flag indicating whether this number is representable by a numeric

Definition at line 158 of file RealAlgebraicNumber.h.

Referenced by do_print(), is_equal_same_type(), isEqual(), GiNaCRA::RealAlgebraicNumber::isNumeric(), operator=(), refine(), and refineAvoiding().

bool GiNaCRA::RealAlgebraicNumber::mIsRoot [protected, inherited]

flag indicating whether this number represents a root of a polynomial or an intermediate point

Definition at line 156 of file RealAlgebraicNumber.h.

Referenced by GiNaCRA::RealAlgebraicNumberNR::do_print(), do_print(), GiNaCRA::RealAlgebraicNumber::isRoot(), GiNaCRA::RealAlgebraicNumber::operator=(), operator=(), and GiNaCRA::RealAlgebraicNumber::setIsRoot().

RationalUnivariatePolynomial GiNaCRA::RealAlgebraicNumberIR::mPolynomial [private]

polynomial of this interval representation

Definition at line 315 of file RealAlgebraicNumberIR.h.

Referenced by add(), calchash(), do_print(), inverse(), minus(), mul(), normalizeInterval(), operator=(), polynomial(), refine(), refineAvoiding(), and sgn().

unsigned GiNaCRA::RealAlgebraicNumberIR::mRefinementCount [private]

number of refinements executed to the isolating interval

Definition at line 321 of file RealAlgebraicNumberIR.h.

Referenced by operator=(), refine(), refineAvoiding(), and refinementCount().

list<RationalUnivariatePolynomial> GiNaCRA::RealAlgebraicNumberIR::mSturmSequence [private]

Standard Sturm sequence of the polynomial and its derivative.

Definition at line 319 of file RealAlgebraicNumberIR.h.

Referenced by normalizeInterval(), operator=(), refine(), refineAvoiding(), and sturmSequence().

numeric GiNaCRA::RealAlgebraicNumber::mValue [protected, inherited]

the exact numeric value of this number if available, otherwise mIsNumeric is false and mValue 0

Definition at line 160 of file RealAlgebraicNumber.h.

Referenced by do_print(), is_equal_same_type(), isEqual(), operator=(), GiNaCRA::RealAlgebraicNumberNR::RealAlgebraicNumberNR(), refine(), refineAvoiding(), and GiNaCRA::RealAlgebraicNumber::value().

The documentation for this class was generated from the following files:

Public Member Functions

Static Public Member Functions

Protected Member Functions

Protected Attributes

Private Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Field Documentation