GiNaCRA  0.6.4
Public Member Functions | Private Types | Private Member Functions | Private Attributes | Friends
GiNaCRA::Groebner Class Reference

Class encapsulating the calculation of Groebner bases. More...

#include <Groebner.h>

Collaboration diagram for GiNaCRA::Groebner:
Collaboration graph
[legend]

Public Member Functions

 Groebner ()
 Groebner (const MultivariatePolynomialMR &p1)
 Creates an ideal with 1 polynomial.
 Groebner (const MultivariatePolynomialMR &p1, const MultivariatePolynomialMR &p2)
 Creates an ideal with 2 polynomials.
 Groebner (const MultivariatePolynomialMR &p1, const MultivariatePolynomialMR &p2, const MultivariatePolynomialMR &p3)
 Creates an ideal with 3 polynomials.
 Groebner (std::list< MultivariatePolynomialMR >::iterator begin_generatingset, std::list< MultivariatePolynomialMR >::iterator end_generatingset)
 Creates an ideal by the list of polynomials.
void addPolynomial (const MultivariatePolynomialMR &p1)
void solve ()
 Reduce the input-ideal to a Groebner basis.
void reduce ()
 Reduces the ideal.
void print () const
 Output the polynomials as expressions.
std::list
< MultivariatePolynomialMR > 		getBase ()
bool isConstant () const
bool isEmpty () const
unsigned size () const
bool isReduced () const
bool isSolved () const
bool hasBeenReduced () const

Private Types

typedef std::list
< MultivariatePolynomialMR >
::iterator 		lpol_It
typedef std::list
< MultivariatePolynomialMR >
::const_iterator 		lpol_cIt

Private Member Functions

void fillB ()

Private Attributes

std::list
< MultivariatePolynomialMR > 		mIdeal
std::list
< MultivariatePolynomialMR > 		mGB
std::list< std::pair< lpol_cIt,
lpol_cIt > > 		pairsToBeChecked
 A list of pairs to be checked.
bool mIsSolved
 A flag whether the basis is solved already.
bool mIsReduced
 A flag whether the basis is reduced already.

Friends

std::ostream & operator<< (std::ostream &os, const Groebner &rhs)
 Output the polynomials in the internal representation.

Detailed Description

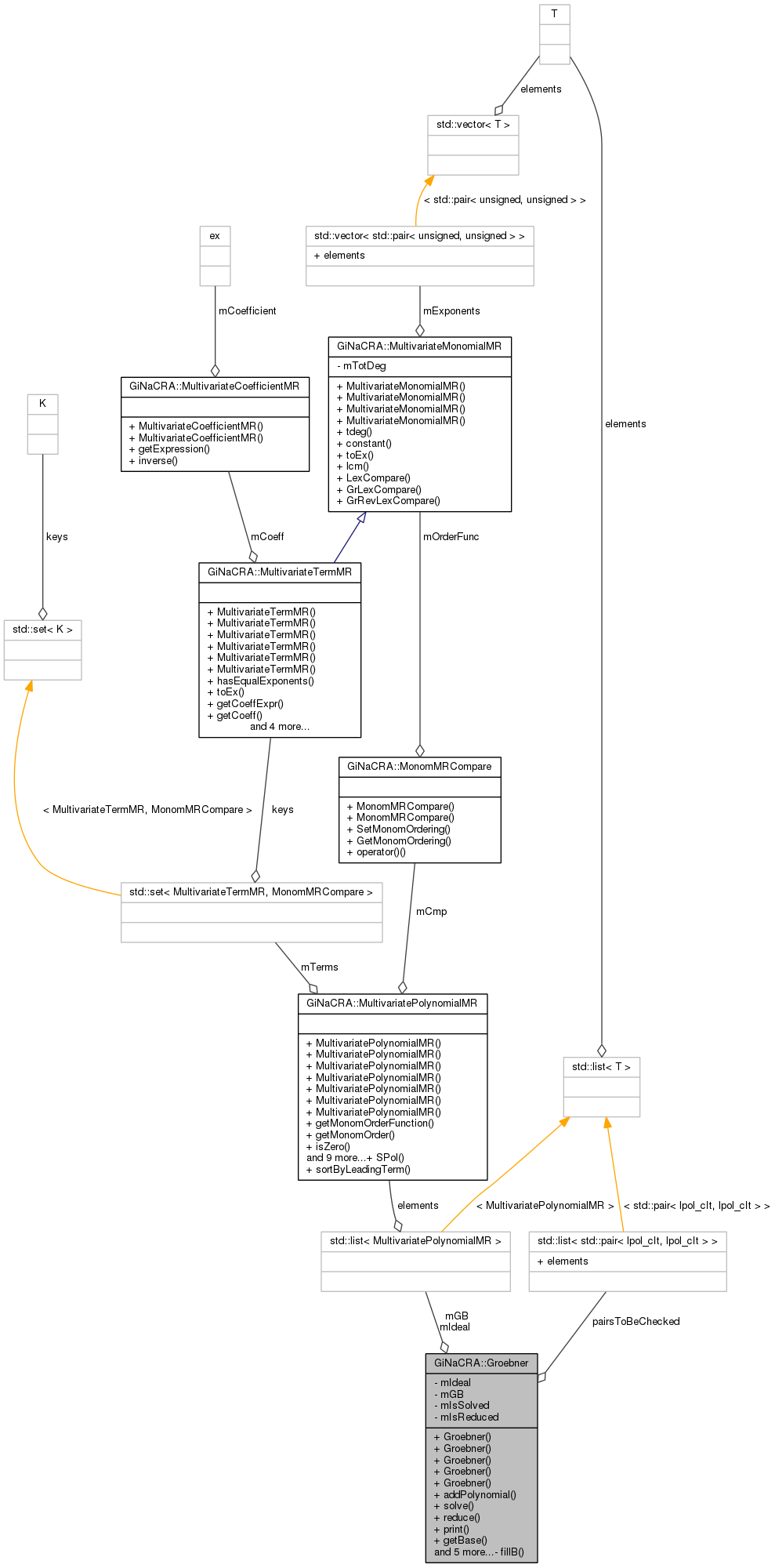
Class encapsulating the calculation of Groebner bases.

Author:
Sebastian Junges
Since:
2011-12-05
Version:
2012-01-19

Definition at line 37 of file Groebner.h.

Member Typedef Documentation

typedef std::list<MultivariatePolynomialMR>::const_iterator GiNaCRA::Groebner::lpol_cIt [private]

Definition at line 162 of file Groebner.h.

typedef std::list<MultivariatePolynomialMR>::iterator GiNaCRA::Groebner::lpol_It [private]

Definition at line 161 of file Groebner.h.

Constructor & Destructor Documentation

GiNaCRA::Groebner::Groebner ( )

Definition at line 31 of file Groebner.cpp.

GiNaCRA::Groebner::Groebner ( const MultivariatePolynomialMR &  p1)

Creates an ideal with 1 polynomial.

Parameters:
p1

Definition at line 36 of file Groebner.cpp.

References mGB, and mIdeal.

GiNaCRA::Groebner::Groebner ( const MultivariatePolynomialMR &  p1,
const MultivariatePolynomialMR &  p2 
)

Creates an ideal with 2 polynomials.

Parameters:
p1
p2

Definition at line 44 of file Groebner.cpp.

References fillB(), mGB, mIdeal, and GiNaCRA::MultivariatePolynomialMR::sortByLeadingTerm().

GiNaCRA::Groebner::Groebner ( const MultivariatePolynomialMR &  p1,
const MultivariatePolynomialMR &  p2,
const MultivariatePolynomialMR &  p3 
)

Creates an ideal with 3 polynomials.

Parameters:
p1
p2
p3

Definition at line 55 of file Groebner.cpp.

References fillB(), mGB, mIdeal, and GiNaCRA::MultivariatePolynomialMR::sortByLeadingTerm().

GiNaCRA::Groebner::Groebner ( std::list< MultivariatePolynomialMR >::iterator  begin_generatingset,
std::list< MultivariatePolynomialMR >::iterator  end_generatingset 
)

Creates an ideal by the list of polynomials.

Parameters:
begin_generatingset
end_generatingset

Definition at line 68 of file Groebner.cpp.

References fillB(), mGB, mIdeal, and GiNaCRA::MultivariatePolynomialMR::sortByLeadingTerm().

Member Function Documentation

void GiNaCRA::Groebner::addPolynomial ( const MultivariatePolynomialMR &  p1)

Definition at line 79 of file Groebner.cpp.

References mGB, mIdeal, mIsReduced, pairsToBeChecked, and GiNaCRA::MultivariatePolynomialMR::sortByLeadingTerm().

Referenced by solve().

void GiNaCRA::Groebner::fillB ( ) [private]

Definition at line 185 of file Groebner.cpp.

References mGB, and pairsToBeChecked.

Referenced by Groebner(), and reduce().

std::list<MultivariatePolynomialMR> GiNaCRA::Groebner::getBase ( ) [inline]

Definition at line 116 of file Groebner.h.

References mGB.

bool GiNaCRA::Groebner::hasBeenReduced ( ) const
Returns:
true, if the GroebnerBase is not equal to the initial ideal

Definition at line 202 of file Groebner.cpp.

References mGB, and mIdeal.

bool GiNaCRA::Groebner::isConstant ( ) const [inline]

Definition at line 121 of file Groebner.h.

References mGB.

bool GiNaCRA::Groebner::isEmpty ( ) const [inline]
Returns:
is there any polynomial in the groebner basis

Definition at line 130 of file Groebner.h.

References mIdeal.

bool GiNaCRA::Groebner::isReduced ( ) const [inline]

Definition at line 144 of file Groebner.h.

References mIsReduced.

bool GiNaCRA::Groebner::isSolved ( ) const [inline]

Definition at line 149 of file Groebner.h.

References pairsToBeChecked.

void GiNaCRA::Groebner::print ( ) const [inline]

Output the polynomials as expressions.

Definition at line 106 of file Groebner.h.

References mGB.

void GiNaCRA::Groebner::reduce ( )

Reduces the ideal.

Definition at line 132 of file Groebner.cpp.

References fillB(), mGB, mIsReduced, and pairsToBeChecked.

unsigned GiNaCRA::Groebner::size ( ) const [inline]
Returns:
how many polynomials are actually in the basis

Definition at line 139 of file Groebner.h.

References mGB.

void GiNaCRA::Groebner::solve ( )

Reduce the input-ideal to a Groebner basis.

This method implements the original Buchberger algorithm.

See also:
ISBN-10: 0387946802, Ch, 2, ยง7

Definition at line 101 of file Groebner.cpp.

References addPolynomial(), GiNaCRA::MultivariatePolynomialMR::CalculateRemainder(), GiNaCRA::MultivariatePolynomialMR::isConstant(), GiNaCRA::MultivariatePolynomialMR::isZero(), mGB, mIsReduced, mIsSolved, pairsToBeChecked, and GiNaCRA::MultivariatePolynomialMR::SPol().

Friends And Related Function Documentation

std::ostream& operator<< ( std::ostream &  os,
const Groebner &  rhs 
) [friend]

Output the polynomials in the internal representation.

Parameters:
os
rhs
Returns:

Definition at line 93 of file Groebner.h.

Field Documentation

std::list<MultivariatePolynomialMR> GiNaCRA::Groebner::mGB [private]

Definition at line 160 of file Groebner.h.

Referenced by addPolynomial(), fillB(), getBase(), Groebner(), hasBeenReduced(), isConstant(), print(), reduce(), size(), and solve().

std::list<MultivariatePolynomialMR> GiNaCRA::Groebner::mIdeal [private]

Definition at line 159 of file Groebner.h.

Referenced by addPolynomial(), Groebner(), hasBeenReduced(), and isEmpty().

bool GiNaCRA::Groebner::mIsReduced [private]

A flag whether the basis is reduced already.

Definition at line 170 of file Groebner.h.

Referenced by addPolynomial(), isReduced(), reduce(), and solve().

bool GiNaCRA::Groebner::mIsSolved [private]

A flag whether the basis is solved already.

Definition at line 168 of file Groebner.h.

Referenced by solve().

std::list<std::pair<lpol_cIt, lpol_cIt> > GiNaCRA::Groebner::pairsToBeChecked [private]

A list of pairs to be checked.

Definition at line 165 of file Groebner.h.

Referenced by addPolynomial(), fillB(), isSolved(), reduce(), and solve().

The documentation for this class was generated from the following files: