 |
GiNaCRA
0.6.4
|
 |
GiNaCRA
0.6.4
|
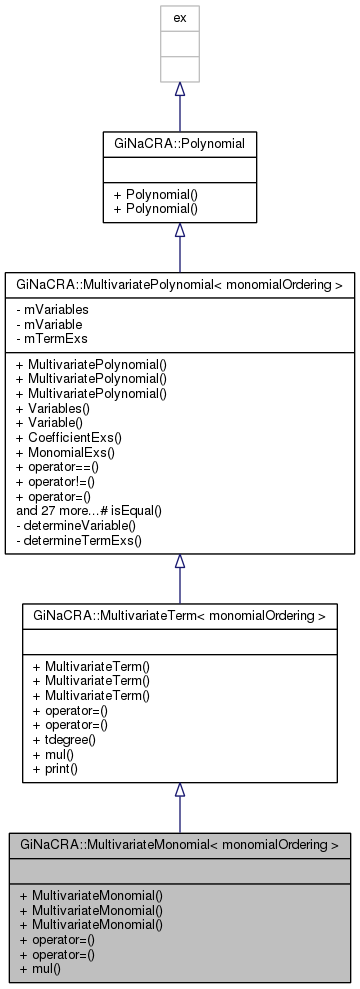
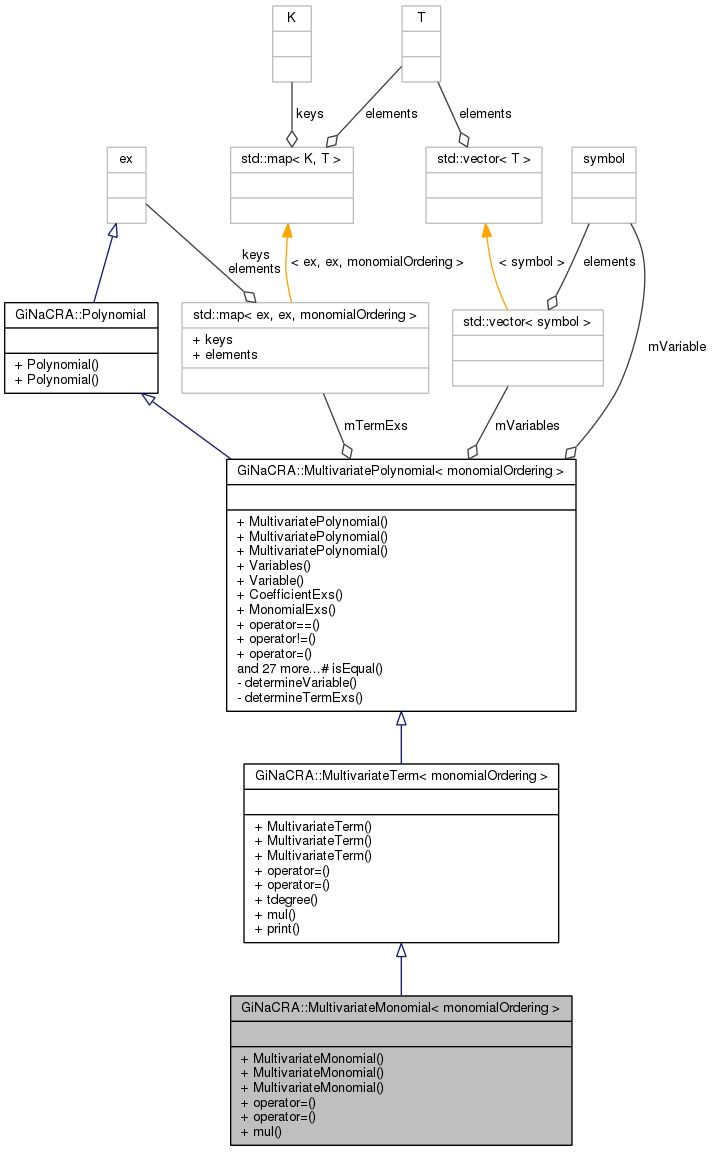
A class for a multivariate monomial providing everything what a GiNaC expression of type power or mul is and, in addition, stores the variables of the monomial (in lexicographic order). More...
#include <MultivariateMonomial.h>
Public Member Functions | |
| MultivariateMonomial () | |
| MultivariateMonomial (const MultivariatePolynomial< monomialOrdering > &p) | |
| Constructs a multivariate monomial as copy of the leading monomial of a MultivariatePolynomial. | |
| MultivariateMonomial (const ex &p, const vector< symbol > &l) throw ( invalid_argument ) | |
| Constructs a multivariate monomial from the given expression, if possible. | |
| const MultivariateMonomial < monomialOrdering > & | operator= (const MultivariateMonomial< monomialOrdering > &) |
| const MultivariateMonomial < monomialOrdering > & | operator= (const ex &) |
| const MultivariateMonomial < monomialOrdering > | mul (const MultivariateMonomial< monomialOrdering > &o) const throw ( invalid_argument ) |
| Multiplies two multivariate monomials and returns a reference to their sum, allocated on the heap. | |
| int | tdegree () const |
| The total degree of the term is the sum of degrees of each symbol. | |
| int | tdegree (const symbol &s) const |
| The total degree of the polynomial w.r.t. | |
| const MultivariateTerm < monomialOrdering > | mul (const MultivariateTerm< monomialOrdering > &o) const throw ( invalid_argument ) |
| Multiplies two multivariate terms and returns a reference to their sum, allocated on the heap. | |
| const MultivariatePolynomial < monomialOrdering > | mul (const MultivariatePolynomial< monomialOrdering > &o) const throw ( invalid_argument ) |
| Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap. | |
| void | print (const print_context &c, unsigned level=0) const |
| const vector< symbol > | Variables () const |
| Selects the list of variables of the polynomial (ordered lexicographicly, not by degree!). | |
| const symbol | Variable () const |
| const list< ex > | CoefficientExs () const |
| Selects the list of polynomial coefficients of this polynomial in the order by the constructor. | |
| const list< ex > | MonomialExs () const |
| Selects the list of monomials of this polynomial in the order by the constructor. | |
| const bool | operator== (const MultivariatePolynomial< monomialOrdering > &) const |
| const bool | operator!= (const MultivariatePolynomial< monomialOrdering > &) const |
| MultivariatePolynomial < monomialOrdering > | diff (const symbol &s, unsigned nth=1) const |
| MultivariatePolynomial < monomialOrdering > | diff (const vector< symbol >::const_iterator i, unsigned nth=1) const |
| MultivariatePolynomial < monomialOrdering > | trunc (const symbol &s) const |
| Removes the leading term w.r.t. | |
| MultivariatePolynomial < monomialOrdering > | trunc () const |
| Removes the leading term. | |
| const MultivariatePolynomial < monomialOrdering > | divideByLcoeff () const |
| Normalizes the polynomial e.g. | |
| int | degree (const symbol &s) const |
| int | degree () const |
| int | ldegree (const symbol &s) const |
| The low-degree is the smallest exponent at the main variable occuring. | |
| int | ldegree () const |
| The low-degree is the smallest exponent at the main variable occuring. | |
| const ex | lterm () const |
| const ex | lcoeff () const |
| const ex | lcoeff (const symbol &s) const |
| const ex | coeff (const symbol &s, const unsigned int &n) const |
| const ex | coeff (const ex &monomial) const throw ( invalid_argument ) |
| const ex | lmon () const |
| bool | isZero () const |
| Returns true if the univariate polynomial is the zero polynomial, otherwise false. | |
| bool | isConstant () const |
| Returns true if the polynomial is constant in the given variables, otherwise false. | |
| const MultivariatePolynomial < monomialOrdering > | reduction (const MultivariatePolynomial< monomialOrdering > &g, const ex &m) const throw ( invalid_argument ) |
| Computes the reduction of this polynomial w.r.t. | |
| const MultivariatePolynomial < monomialOrdering > | normalForm (const list< MultivariatePolynomial< monomialOrdering > > &gb) const throw ( invalid_argument ) |
| Computes the normalform of this polynomial modulo gb. | |
| const MultivariatePolynomial < monomialOrdering > | add (const MultivariatePolynomial< monomialOrdering > &o) const throw ( invalid_argument ) |
| Adds two multivariate polynomials and returns a reference to their sum, allocated on the heap. | |
| const MultivariatePolynomial < monomialOrdering > | minus () const |
| Returns the negative value, allocated on the heap. | |
| const MultivariatePolynomial < monomialOrdering > | pow (const unsigned e) const throw ( invalid_argument ) |
| Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap. | |
| const vector< symbol > | mergeVariables (vector< symbol > l) const |
| Merges this with the given symbol list into a new symbol list. | |
Protected Member Functions | |
| const bool | isEqual (const MultivariatePolynomial< monomialOrdering > &o) const |
A class for a multivariate monomial providing everything what a GiNaC expression of type power or mul is and, in addition, stores the variables of the monomial (in lexicographic order).
It holds: MultivariateCoefficient(vars) * MultivariateMonomial(vars) = MultivariateTerm(vars)
Notation is following http://www.possibility.com/Cpp/CppCodingStandard.html.
Definition at line 42 of file MultivariateMonomial.h.
| GiNaCRA::MultivariateMonomial< monomialOrdering >::MultivariateMonomial | ( | ) |
| GiNaCRA::MultivariateMonomial< monomialOrdering >::MultivariateMonomial | ( | const MultivariatePolynomial< monomialOrdering > & | p | ) |
Constructs a multivariate monomial as copy of the leading monomial of a MultivariatePolynomial.
| p | multivariate polynomial |
| GiNaCRA::MultivariateMonomial< monomialOrdering >::MultivariateMonomial | ( | const ex & | p, |
| const vector< symbol > & | l | ||
| ) | throw ( invalid_argument ) |
Constructs a multivariate monomial from the given expression, if possible.
| p | monomial |
| l | list of the variables of the monomial p |
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::add | ( | const MultivariatePolynomial< monomialOrdering > & | o | ) | const throw ( invalid_argument ) [inherited] |
Adds two multivariate polynomials and returns a reference to their sum, allocated on the heap.
| o |
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::coeff | ( | const symbol & | s, |
| const unsigned int & | n | ||
| ) | const [inherited] |
| n | the exponent |
| s | the main symbol |
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::coeff | ( | const ex & | monomial | ) | const throw ( invalid_argument ) [inherited] |
| invalid_argument | in case the given monomial is not a monomial of this polynomial |
| const list<ex> GiNaCRA::MultivariatePolynomial< monomialOrdering >::CoefficientExs | ( | ) | const [inherited] |
Selects the list of polynomial coefficients of this polynomial in the order by the constructor.
| int GiNaCRA::MultivariatePolynomial< monomialOrdering >::degree | ( | const symbol & | s | ) | const [inherited] |
| s |
Referenced by GiNaCRA::MultivariatePolynomialFactory::searchMonomialsUnderTheStaircase().
| int GiNaCRA::MultivariatePolynomial< monomialOrdering >::degree | ( | ) | const [inherited] |
| MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::diff | ( | const symbol & | s, |
| unsigned | nth = 1 |
||
| ) | const [inherited] |
| s | symbol |
| nth |
Referenced by GiNaCRA::MultivariatePolynomialFactory::specialGroebnerBasis().
| MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::diff | ( | const vector< symbol >::const_iterator | i, |
| unsigned | nth = 1 |
||
| ) | const [inherited] |
| i | iterator pointing to the symbol (in the list of symbols of this MultivariatePolynomial) |
| nth |
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::divideByLcoeff | ( | ) | const [inherited] |
Normalizes the polynomial e.g.
if P = c*(x^2+y^2) in D[x,y] it returns 1*(x^2+y^2).
| bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isConstant | ( | ) | const [inherited] |
Returns true if the polynomial is constant in the given variables, otherwise false.
| const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isEqual | ( | const MultivariatePolynomial< monomialOrdering > & | o | ) | const [inline, protected, inherited] |
| o |
| bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isZero | ( | ) | const [inherited] |
Returns true if the univariate polynomial is the zero polynomial, otherwise false.
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lcoeff | ( | ) | const [inherited] |
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lcoeff | ( | const symbol & | s | ) | const [inherited] |
| s | the variable |
| int GiNaCRA::MultivariatePolynomial< monomialOrdering >::ldegree | ( | const symbol & | s | ) | const [inherited] |
The low-degree is the smallest exponent at the main variable occuring.
| s |
| int GiNaCRA::MultivariatePolynomial< monomialOrdering >::ldegree | ( | ) | const [inherited] |
The low-degree is the smallest exponent at the main variable occuring.
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lmon | ( | ) | const [inherited] |
| const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lterm | ( | ) | const [inherited] |
| const vector<symbol> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mergeVariables | ( | vector< symbol > | l | ) | const [inherited] |
Merges this with the given symbol list into a new symbol list.
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::minus | ( | ) | const [inherited] |
Returns the negative value, allocated on the heap.
| const list<ex> GiNaCRA::MultivariatePolynomial< monomialOrdering >::MonomialExs | ( | ) | const [inherited] |
Selects the list of monomials of this polynomial in the order by the constructor.
| const MultivariateMonomial<monomialOrdering> GiNaCRA::MultivariateMonomial< monomialOrdering >::mul | ( | const MultivariateMonomial< monomialOrdering > & | o | ) | const throw ( invalid_argument ) |
Multiplies two multivariate monomials and returns a reference to their sum, allocated on the heap.
| o |
Referenced by GiNaCRA::MultivariatePolynomialFactory::searchMonomialsUnderTheStaircase().
| const MultivariateTerm<monomialOrdering> GiNaCRA::MultivariateTerm< monomialOrdering >::mul | ( | const MultivariateTerm< monomialOrdering > & | o | ) | const throw ( invalid_argument ) [inherited] |
Multiplies two multivariate terms and returns a reference to their sum, allocated on the heap.
| o |
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mul | ( | const MultivariatePolynomial< monomialOrdering > & | o | ) | const throw ( invalid_argument ) [inherited] |
Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.
| o |
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::normalForm | ( | const list< MultivariatePolynomial< monomialOrdering > > & | gb | ) | const throw ( invalid_argument ) [inherited] |
Computes the normalform of this polynomial modulo gb.
| gb | special Groebner basis of the respective ideal |
| const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator!= | ( | const MultivariatePolynomial< monomialOrdering > & | ) | const [inherited] |
| const MultivariateMonomial<monomialOrdering>& GiNaCRA::MultivariateMonomial< monomialOrdering >::operator= | ( | const MultivariateMonomial< monomialOrdering > & | ) |
| const MultivariateMonomial<monomialOrdering>& GiNaCRA::MultivariateMonomial< monomialOrdering >::operator= | ( | const ex & | ) |
Reimplemented from GiNaCRA::MultivariateTerm< monomialOrdering >.
| const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator== | ( | const MultivariatePolynomial< monomialOrdering > & | ) | const [inherited] |
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::pow | ( | const unsigned | e | ) | const throw ( invalid_argument ) [inherited] |
Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.
| e | exponent |
| void GiNaCRA::MultivariateTerm< monomialOrdering >::print | ( | const print_context & | c, |
| unsigned | level = 0 |
||
| ) | const [inherited] |
Reimplemented from GiNaCRA::MultivariatePolynomial< monomialOrdering >.
| const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::reduction | ( | const MultivariatePolynomial< monomialOrdering > & | g, |
| const ex & | m | ||
| ) | const throw ( invalid_argument ) [inherited] |
Computes the reduction of this polynomial w.r.t.
its monomial m by another polynomial q. This method performs a basic reduction step in computing normal forms modulo a given Groebner basis.
| g | basis polynomial |
| m | monomial of this polynomial w.r.t. which the reduction should take place |
| invalid_argument | in case m is not a monomial of this polynomial |
Referenced by GiNaCRA::MultivariatePolynomialFactory::specialGroebnerBasis().
| int GiNaCRA::MultivariateTerm< monomialOrdering >::tdegree | ( | ) | const [inherited] |
The total degree of the term is the sum of degrees of each symbol.
Reimplemented from GiNaCRA::MultivariatePolynomial< monomialOrdering >.
Referenced by GiNaCRA::MultivariatePolynomialFactory::checkForSpecialGroebnerBasis().
| int GiNaCRA::MultivariatePolynomial< monomialOrdering >::tdegree | ( | const symbol & | s | ) | const [inherited] |
The total degree of the polynomial w.r.t.
the variable s is the maximum sum of degrees of each monomial containing the variable s.
| s | variable |
| MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::trunc | ( | const symbol & | s | ) | const [inherited] |
Removes the leading term w.r.t.
one variable.
| s | the variable |
| MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::trunc | ( | ) | const [inherited] |
Removes the leading term.
| const symbol GiNaCRA::MultivariatePolynomial< monomialOrdering >::Variable | ( | ) | const [inherited] |
| const vector<symbol> GiNaCRA::MultivariatePolynomial< monomialOrdering >::Variables | ( | ) | const [inherited] |
Selects the list of variables of the polynomial (ordered lexicographicly, not by degree!).
Referenced by GiNaCRA::MultivariatePolynomialFactory::searchMonomialsUnderTheStaircase(), and GiNaCRA::MultivariatePolynomialFactory::synthesizeSpecialGroebnerBasisDegrees().