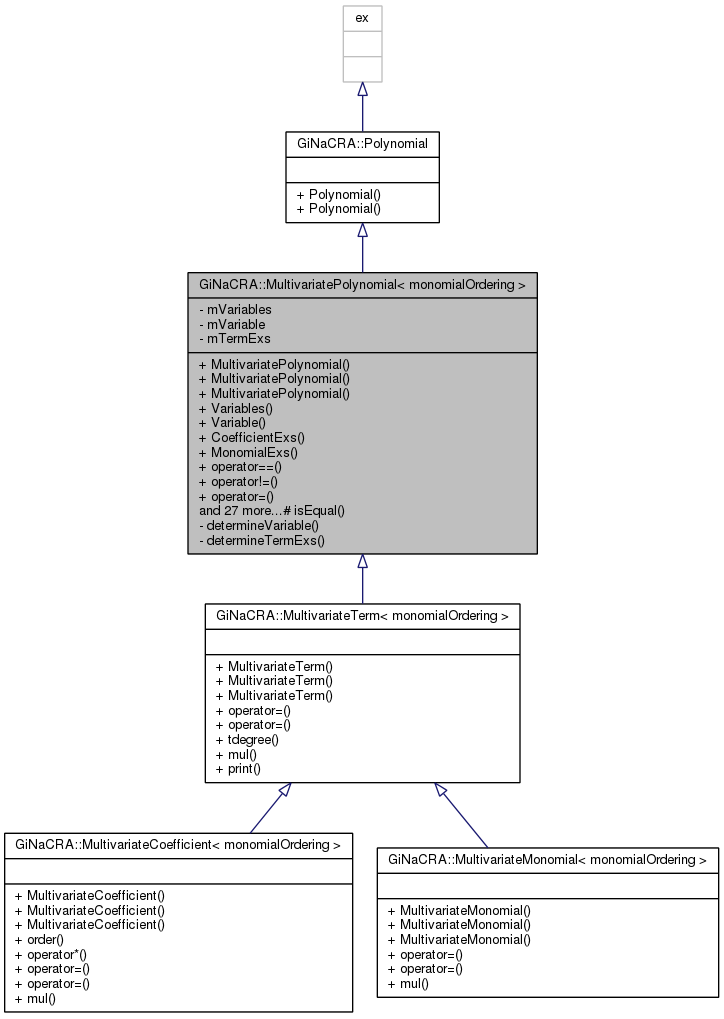
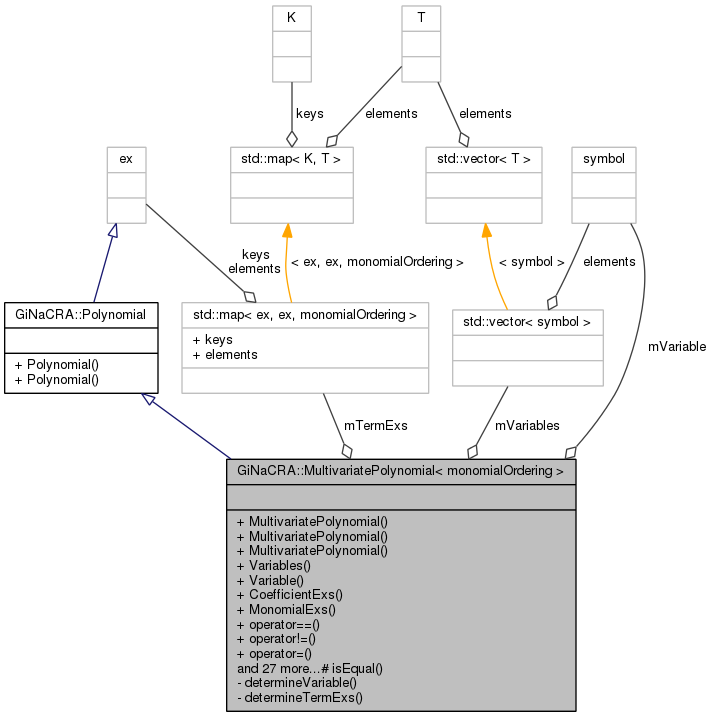
A class for a multivariate polynomial providing everything what a GiNaC expression of type polynomial is and, in addition, stores the variables of the polynomial (in lexicographic order) as well as the leading term in the variable with the maximal degree. More...

#include <MultivariatePolynomial.h>

Inheritance diagram for GiNaCRA::MultivariatePolynomial< monomialOrdering >:

[legend]

Collaboration diagram for GiNaCRA::MultivariatePolynomial< monomialOrdering >:

[legend]

Public Member Functions
	MultivariatePolynomial ()
	Constructs a multivariate polynomial consisting of the standard variable defined in constants.h.
	MultivariatePolynomial (const MultivariatePolynomial< monomialOrdering > &p)
	Constructs a multivariate polynomial as copy of another one.
	MultivariatePolynomial (const ex &p, const vector< symbol > &l) throw ( invalid_argument )
	Constructs a multivariate polynomial using graded degree lexicographic monomial ordering.
const vector< symbol >	Variables () const
	Selects the list of variables of the polynomial (ordered lexicographicly, not by degree!).
const symbol	Variable () const
const list< ex >	CoefficientExs () const
	Selects the list of polynomial coefficients of this polynomial in the order by the constructor.
const list< ex >	MonomialExs () const
	Selects the list of monomials of this polynomial in the order by the constructor.
const bool	operator== (const MultivariatePolynomial< monomialOrdering > &) const
const bool	operator!= (const MultivariatePolynomial< monomialOrdering > &) const
const MultivariatePolynomial < monomialOrdering > &	operator= (const MultivariatePolynomial< monomialOrdering > &)
const MultivariatePolynomial < monomialOrdering > &	operator= (const ex &)
MultivariatePolynomial < monomialOrdering >	diff (const symbol &s, unsigned nth=1) const
MultivariatePolynomial < monomialOrdering >	diff (const vector< symbol >::const_iterator i, unsigned nth=1) const
MultivariatePolynomial < monomialOrdering >	trunc (const symbol &s) const
	Removes the leading term w.r.t.
MultivariatePolynomial < monomialOrdering >	trunc () const
	Removes the leading term.
const MultivariatePolynomial < monomialOrdering >	divideByLcoeff () const
	Normalizes the polynomial e.g.
int	degree (const symbol &s) const
int	degree () const
int	ldegree (const symbol &s) const
	The low-degree is the smallest exponent at the main variable occuring.
int	ldegree () const
	The low-degree is the smallest exponent at the main variable occuring.
int	tdegree () const
	The total degree of the polynomial is the maximum sum of degrees of each monomial.
int	tdegree (const symbol &s) const
	The total degree of the polynomial w.r.t.
const ex	lterm () const
const ex	lcoeff () const
const ex	coeff (const symbol &s, const unsigned int &n) const
const ex	lcoeff (const symbol &s) const
const ex	coeff (const ex &monomial) const throw ( invalid_argument )
const ex	lmon () const
bool	isZero () const
	Returns true if the univariate polynomial is the zero polynomial, otherwise false.
bool	isConstant () const
	Returns true if the polynomial is constant in the given variables, otherwise false.
const MultivariatePolynomial < monomialOrdering >	reduction (const MultivariatePolynomial< monomialOrdering > &g, const ex &m) const throw ( invalid_argument )
	Computes the reduction of this polynomial w.r.t.
const MultivariatePolynomial < monomialOrdering >	normalForm (const list< MultivariatePolynomial< monomialOrdering > > &gb) const throw ( invalid_argument )
	Computes the normalform of this polynomial modulo gb.
const MultivariatePolynomial < monomialOrdering >	add (const MultivariatePolynomial< monomialOrdering > &o) const throw ( invalid_argument )
	Adds two multivariate polynomials and returns a reference to their sum, allocated on the heap.
const MultivariatePolynomial < monomialOrdering >	minus () const
	Returns the negative value, allocated on the heap.
const MultivariatePolynomial < monomialOrdering >	mul (const MultivariatePolynomial< monomialOrdering > &o) const throw ( invalid_argument )
	Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.
const MultivariatePolynomial < monomialOrdering >	pow (const unsigned e) const throw ( invalid_argument )
	Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.
void	print (const print_context &c, unsigned level=0) const
const vector< symbol >	mergeVariables (vector< symbol > l) const
	Merges this with the given symbol list into a new symbol list.
Protected Member Functions
const bool	isEqual (const MultivariatePolynomial< monomialOrdering > &o) const
Private Member Functions
const symbol	determineVariable () const
const std::map< ex, ex, monomialOrdering >	determineTermExs () const
Private Attributes
vector< symbol >	mVariables
symbol	mVariable
std::map< ex, ex, monomialOrdering >	mTermExs
Friends
class	MultivariateTerm
class	MultivariateMonomial
class	MultivariateCoefficient

Detailed Description

template<class monomialOrdering>
class GiNaCRA::MultivariatePolynomial< monomialOrdering >

A class for a multivariate polynomial providing everything what a GiNaC expression of type polynomial is and, in addition, stores the variables of the polynomial (in lexicographic order) as well as the leading term in the variable with the maximal degree.

Author:: Ulrich Loup

Since:: 2010-11-01

Version:: 2011-11-03

See also:: ISBN 0-387-94090-1 and ISBN-13: 978-3642069642

Notation is following http://www.possibility.com/Cpp/CppCodingStandard.html.

Definition at line 48 of file MultivariatePolynomial.h.

Constructor & Destructor Documentation

template<class monomialOrdering>

GiNaCRA::MultivariatePolynomial< monomialOrdering >::MultivariatePolynomial ( )

Constructs a multivariate polynomial consisting of the standard variable defined in constants.h.

template<class monomialOrdering>

GiNaCRA::MultivariatePolynomial< monomialOrdering >::MultivariatePolynomial ( const MultivariatePolynomial< monomialOrdering > & p )

Constructs a multivariate polynomial as copy of another one.

Parameters:

p	multivariate polynomial

template<class monomialOrdering>

GiNaCRA::MultivariatePolynomial< monomialOrdering >::MultivariatePolynomial	(	const ex &	p,
		const vector< symbol > &	l
	)		throw ( invalid_argument )

Constructs a multivariate polynomial using graded degree lexicographic monomial ordering.

Parameters:

p	polynomial
l	list of the variables of the polynomial p

Member Function Documentation

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::add ( const MultivariatePolynomial< monomialOrdering > & o ) const throw ( invalid_argument )

Adds two multivariate polynomials and returns a reference to their sum, allocated on the heap.

Parameters:

o

Returns:: sum allocated on the heap

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::coeff	(	const symbol &	s,
		const unsigned int &	n
	)		const

Parameters:

n	the exponent
s	the main symbol

Returns:: coefficient in front of s^n

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::coeff ( const ex & monomial ) const throw ( invalid_argument )

Returns:: coefficient in front of the given monomial w.r.t. the given monomial ordering

Exceptions:

invalid_argument in case the given monomial is not a monomial of this polynomial

template<class monomialOrdering>

const list<ex> GiNaCRA::MultivariatePolynomial< monomialOrdering >::CoefficientExs ( ) const

Selects the list of polynomial coefficients of this polynomial in the order by the constructor.

Returns:: list of polynomial coefficients of this polynomial

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::degree ( const symbol & s ) const

Parameters:

s

Returns:: degree of the univariate polynomial in the given symbol

Referenced by GiNaCRA::MultivariatePolynomialFactory::searchMonomialsUnderTheStaircase().

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::degree ( ) const

Returns:: degree of the univariate polynomial in the main symbol

template<class monomialOrdering>

const std::map<ex, ex, monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::determineTermExs ( ) const [private]

Returns:: the list of monomials coupled with their coefficients of this polynomial in the given monomial order

template<class monomialOrdering>

const symbol GiNaCRA::MultivariatePolynomial< monomialOrdering >::determineVariable ( ) const [private]

Returns:: index of the (or one of the) symbols of the polynomial with maximal degree

template<class monomialOrdering>

MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::diff	(	const symbol &	s,
		unsigned	nth = `1`
	)		const

Parameters:

s	symbol
nth

Returns:: nth derivative of the univariate polynomial in the given symbol

Referenced by GiNaCRA::MultivariatePolynomialFactory::specialGroebnerBasis().

template<class monomialOrdering>

MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::diff	(	const vector< symbol >::const_iterator	i,
		unsigned	nth = `1`
	)		const

Parameters:

i	iterator pointing to the symbol (in the list of symbols of this MultivariatePolynomial)
nth

Returns:: nth derivative of the univariate polynomial in the given symbol

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::divideByLcoeff ( ) const

Normalizes the polynomial e.g.

if P = c*(x^2+y^2) in D[x,y] it returns 1*(x^2+y^2).

Returns:: normalized polynomial

template<class monomialOrdering>

bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isConstant ( ) const

Returns true if the polynomial is constant in the given variables, otherwise false.

Returns:: true if the polynomial is constant, otherwise false

template<class monomialOrdering>

const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isEqual ( const MultivariatePolynomial< monomialOrdering > & o ) const [inline, protected]

Parameters:

o

Returns:: true in case the other multivariate polynomial equals this

template<class monomialOrdering>

bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::isZero ( ) const

Returns true if the univariate polynomial is the zero polynomial, otherwise false.

Returns:: true if the univariate polynomial is the zero polynomial, otherwise false.

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lcoeff ( ) const

Returns:: coefficient in front of the monomial at the highest position in the given monomial ordering

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lcoeff ( const symbol & s ) const

Parameters:

s	the variable

Returns:: the leading coefficient with respect to a variable x

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::ldegree ( const symbol & s ) const

The low-degree is the smallest exponent at the main variable occuring.

Parameters:

s

Returns:: low-degree of the univariate polynomial in the given symbol

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::ldegree ( ) const

The low-degree is the smallest exponent at the main variable occuring.

Returns:: low-degree of the univariate polynomial in the main symbol

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lmon ( ) const

Returns:: monomial at the highest position according to the monomial ordering

template<class monomialOrdering>

const ex GiNaCRA::MultivariatePolynomial< monomialOrdering >::lterm ( ) const

Returns:: lcoeff * lmon

template<class monomialOrdering>

const vector<symbol> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mergeVariables ( vector< symbol > l ) const

Merges this with the given symbol list into a new symbol list.

Returns:: new symbol list containing both this and the other symbols

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::minus ( ) const

Returns the negative value, allocated on the heap.

Returns:: negative value allocated on the heap

template<class monomialOrdering>

const list<ex> GiNaCRA::MultivariatePolynomial< monomialOrdering >::MonomialExs ( ) const

Selects the list of monomials of this polynomial in the order by the constructor.

Returns:: list of monomials of this polynomial

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mul ( const MultivariatePolynomial< monomialOrdering > & o ) const throw ( invalid_argument )

Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.

Parameters:

o

Returns:: product allocated on the heap

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::normalForm ( const list< MultivariatePolynomial< monomialOrdering > > & gb ) const throw ( invalid_argument )

Computes the normalform of this polynomial modulo gb.

Parameters:

gb	special Groebner basis of the respective ideal

Returns:: normalform of this polynomial modulo gb

See also:: Algorithm 12.2 in ISBN-13: 978-3642069642

template<class monomialOrdering>

const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator!= ( const MultivariatePolynomial< monomialOrdering > & ) const

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering>& GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator= ( const MultivariatePolynomial< monomialOrdering > & )

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering>& GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator= ( const ex & )

Reimplemented in GiNaCRA::MultivariateCoefficient< monomialOrdering >, GiNaCRA::MultivariateMonomial< monomialOrdering >, and GiNaCRA::MultivariateTerm< monomialOrdering >.

template<class monomialOrdering>

const bool GiNaCRA::MultivariatePolynomial< monomialOrdering >::operator== ( const MultivariatePolynomial< monomialOrdering > & ) const

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::pow ( const unsigned e ) const throw ( invalid_argument )

Multiplies two multivariate polynomials and returns a reference to their product, allocated on the heap.

Parameters:

e exponent

Returns:: power of this polynomial to e

template<class monomialOrdering>

void GiNaCRA::MultivariatePolynomial< monomialOrdering >::print	(	const print_context &	c,
		unsigned	level = `0`
	)		const

Reimplemented in GiNaCRA::MultivariateTerm< monomialOrdering >.

template<class monomialOrdering>

const MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::reduction	(	const MultivariatePolynomial< monomialOrdering > &	g,
		const ex &	m
	)		const throw ( invalid_argument )

Computes the reduction of this polynomial w.r.t.

its monomial m by another polynomial q. This method performs a basic reduction step in computing normal forms modulo a given Groebner basis.

Parameters:

g	basis polynomial
m	monomial of this polynomial w.r.t. which the reduction should take place

Returns:: reduction modulo q w.r.t. m

Exceptions:

invalid_argument in case m is not a monomial of this polynomial

See also:: Definition 4.64 in ISBN-13: 978-3642069642

Referenced by GiNaCRA::MultivariatePolynomialFactory::specialGroebnerBasis().

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::tdegree ( ) const

The total degree of the polynomial is the maximum sum of degrees of each monomial.

Returns:: total degree of the MultivariatePolynomial

See also:: page 136 in ISBN 0-387-94090-1 and ISBN-13: 978-3642069642

Reimplemented in GiNaCRA::MultivariateTerm< monomialOrdering >.

Referenced by GiNaCRA::MultivariatePolynomialFactory::synthesizeSpecialGroebnerBasisDegrees().

template<class monomialOrdering>

int GiNaCRA::MultivariatePolynomial< monomialOrdering >::tdegree ( const symbol & s ) const

The total degree of the polynomial w.r.t.

the variable s is the maximum sum of degrees of each monomial containing the variable s.

Parameters:

s variable

Returns:: total degree of the MultivariatePolynomial

See also:: page 485 in ISBN 0-387-94090-1 and ISBN-13: 978-3642069642

template<class monomialOrdering>

MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::trunc ( const symbol & s ) const

Removes the leading term w.r.t.

one variable.

Parameters:

s	the variable

Returns:: the polynomial without leading term

template<class monomialOrdering>

MultivariatePolynomial<monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::trunc ( ) const

Removes the leading term.

Returns:: the polynomial without leading term

template<class monomialOrdering>

const symbol GiNaCRA::MultivariatePolynomial< monomialOrdering >::Variable ( ) const

Returns:: the (or one of the) symbols of the polynomial with maximal degree

template<class monomialOrdering>

const vector<symbol> GiNaCRA::MultivariatePolynomial< monomialOrdering >::Variables ( ) const

Selects the list of variables of the polynomial (ordered lexicographicly, not by degree!).

Returns:: list of symbols

Referenced by GiNaCRA::MultivariatePolynomialFactory::searchMonomialsUnderTheStaircase(), and GiNaCRA::MultivariatePolynomialFactory::synthesizeSpecialGroebnerBasisDegrees().

Friends And Related Function Documentation

template<class monomialOrdering>

friend class MultivariateCoefficient [friend]

Definition at line 56 of file MultivariatePolynomial.h.

template<class monomialOrdering>

friend class MultivariateMonomial [friend]

Definition at line 54 of file MultivariatePolynomial.h.

template<class monomialOrdering>

friend class MultivariateTerm [friend]

Definition at line 52 of file MultivariatePolynomial.h.

Field Documentation

template<class monomialOrdering>

std::map<ex, ex, monomialOrdering> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mTermExs [private]

Definition at line 331 of file MultivariatePolynomial.h.

template<class monomialOrdering>

symbol GiNaCRA::MultivariatePolynomial< monomialOrdering >::mVariable [private]

Definition at line 330 of file MultivariatePolynomial.h.

template<class monomialOrdering>

vector<symbol> GiNaCRA::MultivariatePolynomial< monomialOrdering >::mVariables [private]

Definition at line 329 of file MultivariatePolynomial.h.

The documentation for this class was generated from the following file:

MultivariatePolynomial.h

Public Member Functions

Protected Member Functions

Private Member Functions

Private Attributes

Friends

Detailed Description

template<class monomialOrdering> class GiNaCRA::MultivariatePolynomial< monomialOrdering >

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Field Documentation

template<class monomialOrdering>
class GiNaCRA::MultivariatePolynomial< monomialOrdering >