GiNaCRA  0.6.4
Public Member Functions | Protected Member Functions | Private Member Functions | Private Attributes
GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering > Class Template Reference

A class providing the multiplication table for the quotient ring modulo a given Groebner basis. More...

#include <SpecialQuotientRingMultiplicationTable.h>

Collaboration diagram for GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >:
Collaboration graph
[legend]

Public Member Functions

 SpecialQuotientRingMultiplicationTable (list< MultivariatePolynomial< monomialOrdering > > gb) throw ( invalid_argument )
 Constructs a multiplication table according to the given zero-dimensional Groebner basis.
 SpecialQuotientRingMultiplicationTable (MultivariatePolynomial< monomialOrdering > p)
 Constructs a multiplication table according to the zero-dimensional Groebner basis which is constructed from the given polynomial as a special Groebner basis w.r.t.
const list
< MultivariatePolynomial
< monomialOrdering > > 		GroebnerBasis () const
 Get the special Groebner basis of the ideal spanning the quotient ring.
const vector< MultivariateTerm
< monomialOrdering > > 		TermsUnderTheStaircase () const
 Get the monomials under the staircase.
const int dim () const
 Get the number of monomials under the staircase, that is, the dimension of the vector space.
const list< symbol > Variables () const
const bool operator== (const SpecialQuotientRingMultiplicationTable< monomialOrdering > &) const
const bool operator!= (const SpecialQuotientRingMultiplicationTable< monomialOrdering > &) const
const MultivariatePolynomial
< monomialOrdering > 		product (const MultivariateTerm< monomialOrdering > m1, const MultivariateTerm< monomialOrdering > m2) const throw ( invalid_argument )
 Efficiently compute m1 * m2 within the quotient ring.
const MultivariatePolynomial
< monomialOrdering > 		product (const int i, const int j) const throw ( invalid_argument )
 Efficiently compute the product of the i-th and the j-th basis element within the quotient ring.
void realRoots () const
 Compute the roots of the input polynomial.
std::ostream & print (std::ostream &os) const

Protected Member Functions

const bool isEqual (const SpecialQuotientRingMultiplicationTable< monomialOrdering > &o) const
const MultivariatePolynomial
< monomialOrdering > 		trace (const MultivariatePolynomial< monomialOrdering > p) const throw ( invalid_argument )
 Efficiently compute the trace of the linear form L_p where p is a special template polynomial.
const MultivariatePolynomial
< monomialOrdering > 		generalPositionTemplatePowerTrace (const numeric &i, const unsigned e) const throw ( invalid_argument )
 Compute the trace of the general position template of index i (without constant part) to the power of e.

Private Member Functions

void initializeMultiplicationTable ()
 Computes the coefficients of the normal forms of all products of basis elements.
void initializeBasis ()
 Creates mTermsUnderTheStaircase and sorts it according to monomialOrdering.

Private Attributes

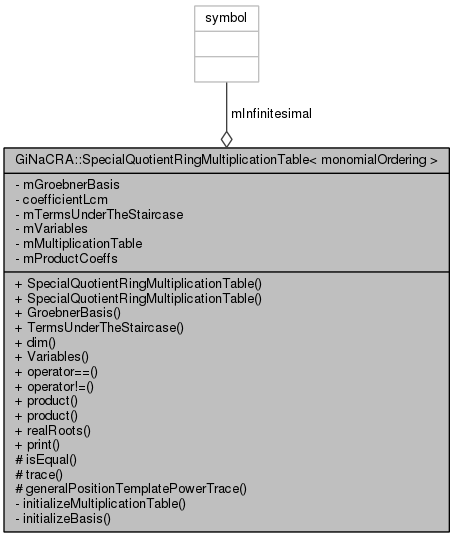
symbol mInfinitesimal
list< MultivariatePolynomial
< monomialOrdering > > 		mGroebnerBasis
MultivariateCoefficient
< monomialOrdering > 		coefficientLcm
vector< MultivariateTerm
< monomialOrdering > > 		mTermsUnderTheStaircase
list< symbol > mVariables
map< pair< pair< int, int >
, int >, set< ex, ex_is_less >
::iterator > 		mMultiplicationTable
set< ex, ex_is_less > mProductCoeffs

Detailed Description

template<class monomialOrdering>
class GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >

A class providing the multiplication table for the quotient ring modulo a given Groebner basis.

In the constructor the following is performed:

  • Check/construction of a special Groebner basis.
  • Computation of the terms under the staircase as the vector space/quotient ring basis of the quotient ring modulo the ideal generated by the given Groebner basis.
  • Computation of each product of two basis elements as linear combination of the basis elements.

The multiplication table is stored as a map. With a slight loss of efficiency for accessing the entries (O(log(t) if t is the number of entries), this representation is a good more memory efficient than a three-dimensional array.

Runtime complexities in a nutshell: Let n be the number of monomial basis elements and t be the number of multiplication table entries. This class implements the vector representation of the monomial basis.<br/ >

  • Product of two monomials as terms: O(log(n)*n*log(t)) for vector, O(n^3) for list implementation
  • Product of two monomials as indices: O(n*log(t)) for both vector and list implementation
  • Trace computation: O(n^2*log(t)) for both vector and list implementation
  • Printing the multiplication table: O(n^3*log(t)) for both vector and list implementation
Author:
Ulrich Loup
Since:
2011-07-11
Version:
2011-10-26
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642

Notation is following http://www.possibility.com/Cpp/CppCodingStandard.html.

Definition at line 58 of file SpecialQuotientRingMultiplicationTable.h.

Constructor & Destructor Documentation

template<class monomialOrdering>
GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::SpecialQuotientRingMultiplicationTable ( list< MultivariatePolynomial< monomialOrdering > >  gb) throw ( invalid_argument )

Constructs a multiplication table according to the given zero-dimensional Groebner basis.

Parameters:
gba special Groebner basis
Exceptions:
invalid_argumentin case gb was not special
template<class monomialOrdering>
GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::SpecialQuotientRingMultiplicationTable ( MultivariatePolynomial< monomialOrdering >  p)

Constructs a multiplication table according to the zero-dimensional Groebner basis which is constructed from the given polynomial as a special Groebner basis w.r.t.

radius 1 and the infinitesimal varZeta.

Parameters:
pa polynomial

Member Function Documentation

template<class monomialOrdering>
const int GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::dim ( ) const [inline]

Get the number of monomials under the staircase, that is, the dimension of the vector space.

Returns:
the dimension of the vector space, that is, the number of basis elements
template<class monomialOrdering>
const MultivariatePolynomial<monomialOrdering> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::generalPositionTemplatePowerTrace ( const numeric &  i,
const unsigned  e 
) const throw ( invalid_argument ) [inline, protected]

Compute the trace of the general position template of index i (without constant part) to the power of e.

Parameters:
iindex of the general position template
epower to which the template polynomial is raised
Returns:
trace of the general position template of index i (without constant part) to the power of e
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642, in Algorithm 12.14
Exceptions:
errorif the input did not happen to show the correct coefficient structure
template<class monomialOrdering>
const list<MultivariatePolynomial<monomialOrdering> > GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::GroebnerBasis ( ) const

Get the special Groebner basis of the ideal spanning the quotient ring.

Returns:
the special Groebner basis of the ideal spanning the quotient ring
template<class monomialOrdering>
void GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::initializeBasis ( ) [inline, private]

Creates mTermsUnderTheStaircase and sorts it according to monomialOrdering.

template<class monomialOrdering>
void GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::initializeMultiplicationTable ( ) [inline, private]

Computes the coefficients of the normal forms of all products of basis elements.

Todo:
This version of the algorithm is implemented straight-forward. A more sophisticated approach can be found on page 457 of ISBN 0-387-94090-1.
template<class monomialOrdering>
const bool GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::isEqual ( const SpecialQuotientRingMultiplicationTable< monomialOrdering > &  o) const [inline, protected]
Parameters:
o
Returns:
true in case the other multivariate polynomial equals this
template<class monomialOrdering>
const bool GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::operator!= ( const SpecialQuotientRingMultiplicationTable< monomialOrdering > &  ) const
template<class monomialOrdering>
const bool GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::operator== ( const SpecialQuotientRingMultiplicationTable< monomialOrdering > &  ) const
template<class monomialOrdering>
std::ostream& GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::print ( std::ostream &  os) const
Parameters:
os
Returns:
new output stream containing the information of this multiplication table
template<class monomialOrdering>
const MultivariatePolynomial<monomialOrdering> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::product ( const MultivariateTerm< monomialOrdering >  m1,
const MultivariateTerm< monomialOrdering >  m2 
) const throw ( invalid_argument )

Efficiently compute m1 * m2 within the quotient ring.

Parameters:
m1
m2
Returns:
the product of m1 and m2 modulo the given Groebner basis
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642, Algorithm 12.4
template<class monomialOrdering>
const MultivariatePolynomial<monomialOrdering> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::product ( const int  i,
const int  j 
) const throw ( invalid_argument ) [inline]

Efficiently compute the product of the i-th and the j-th basis element within the quotient ring.

Parameters:
i
j
Returns:
the product of the i-th and the j-th basis element modulo the given Groebner basis
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642, Algorithm 12.4
template<class monomialOrdering>
void GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::realRoots ( ) const

Compute the roots of the input polynomial.

Returns:
roots of the input polynomial
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642, Algorithm 12.14
template<class monomialOrdering>
const vector<MultivariateTerm<monomialOrdering> > GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::TermsUnderTheStaircase ( ) const

Get the monomials under the staircase.

This is the basis of the quotient ring. It is sorted according to monomialOrdering.

Returns:
the terms under the staircase according to the ideal defined by the input Groebner basis sorted according to monomialOrdering
template<class monomialOrdering>
const MultivariatePolynomial<monomialOrdering> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::trace ( const MultivariatePolynomial< monomialOrdering >  p) const throw ( invalid_argument ) [inline, protected]

Efficiently compute the trace of the linear form L_p where p is a special template polynomial.

The trace is the sum of the main diagonal of the matrix associated with the linear form of p mapping each a to p*a.

Parameters:
p
Returns:
trace of the linear map p* (left-multiplication with p) w.r.t. this basis
See also:
ISBN 0-387-94090-1 and ISBN-13: 978-3642069642, Algorithm 12.5
Exceptions:
errorif the input did not happen to show the correct coefficient structure
template<class monomialOrdering>
const list<symbol> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::Variables ( ) const
Returns:
the list of variables of this quotient ring

Field Documentation

template<class monomialOrdering>
MultivariateCoefficient<monomialOrdering> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::coefficientLcm [private]

Definition at line 188 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
list<MultivariatePolynomial<monomialOrdering> > GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mGroebnerBasis [private]

Definition at line 187 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
symbol GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mInfinitesimal [private]

Definition at line 186 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
map<pair<pair<int, int>, int>, set<ex, ex_is_less>::iterator> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mMultiplicationTable [private]

Definition at line 192 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
set<ex, ex_is_less> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mProductCoeffs [private]

Definition at line 193 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
vector<MultivariateTerm<monomialOrdering> > GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mTermsUnderTheStaircase [private]

Definition at line 189 of file SpecialQuotientRingMultiplicationTable.h.

template<class monomialOrdering>
list<symbol> GiNaCRA::SpecialQuotientRingMultiplicationTable< monomialOrdering >::mVariables [private]

Definition at line 190 of file SpecialQuotientRingMultiplicationTable.h.

The documentation for this class was generated from the following file: